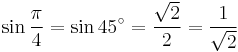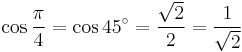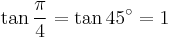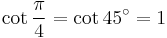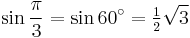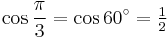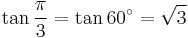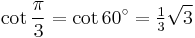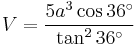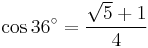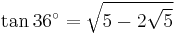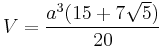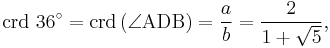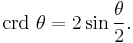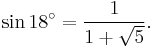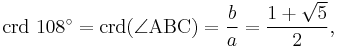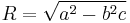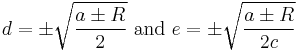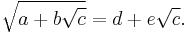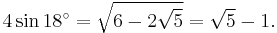Exact trigonometric constants
Exact constant expressions for trigonometric values are sometimes useful, mainly for simplifying solutions into radical forms which allow further simplification.
All values of sine, cosine, and tangent of angles with 3° increments are derivable using identities: half-angle, double-angle, addition/subtraction and values for 0°, 30°, 36°, and 45°. Note that 1° = π/180 radians.
According to Niven's theorem, the only rational values of the sine function for which the argument is a rational number of degrees are 0, 1/2, and 1.
Fermat number
This article is incomplete in at least two senses. First, it is always possible to apply a half-angle formula and find an exact expression for the cosine of one-half the smallest angle on the list. Second, this article exploits only the first two of five known Fermat primes: 3 and 5; and the trigonometric functions of other angles, such as 2π/7, 2π/9 (= 40°), and 2π/13 (as well as the other constructible polygons, 2π/17, 2π/257, or 2π/65537) are soluble by radicals. In practice, all values of sine, cosine, and tangent not found in this article are approximated using the techniques described at Generating trigonometric tables.
Table of constants
Values outside the [0°, 45°] angle range are trivially derived from these values, using circle axis reflection symmetry. (See Trigonometric identity.)
0°: fundamental
3°: 60-sided polygon
6°: 30-sided polygon
9°: 20-sided polygon
12°: 15-sided polygon
15°: dodecagon
18°: decagon
21°: sum 9° + 12°
22.5°: octagon
24°: sum 12° + 12°
27°: sum 12° + 15°
30°: hexagon
33°: sum 15° + 18°
36°: pentagon
39°: sum 18° + 21°
42°: sum 21° + 21°
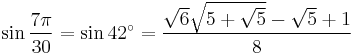
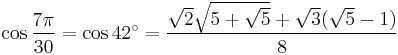
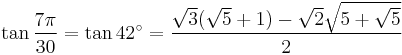 {
{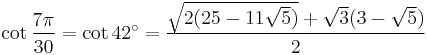
45°: square
60°: triangle
where  is the golden ratio.
is the golden ratio.
Notes
Uses for constants
As an example of the use of these constants, consider a dodecahedron with the following volume, where a is the length of an edge:
Using
this can be simplified to:
Derivation triangles
The derivation of sine, cosine, and tangent constants into radial forms is based upon the constructibility of right triangles.
Here right triangles made from symmetry sections of regular polygons are used to calculate fundamental trigonometric ratios. Each right triangle represents three points in a regular polygon: a vertex, an edge center containing that vertex, and the polygon center. An n-gon can be divided into 2n right triangles with angles of {180/n, 90−180/n, 90} degrees, for n in 3, 4, 5, ...
Constructibility of 3, 4, 5, and 15-sided polygons are the basis, and angle bisectors allow multiples of two to also be derived.
- Constructible
- 3×2n-sided regular polygons, for n in 0, 1, 2, 3, ...
- 30°-60°-90° triangle: triangle (3-sided)
- 60°-30°-90° triangle: hexagon (6-sided)
- 75°-15°-90° triangle: dodecagon (12-sided)
- 82.5°-7.5°-90° triangle: icosikaitetragon (24-sided)
- 86.25°-3.75°-90° triangle: tetracontakaioctagon (48-sided)
- ...
- 4×2n-sided
- 45°-45°-90° triangle: square (4-sided)
- 67.5°-22.5°-90° triangle: octagon (8-sided)
- 78.75°-11.25°-90° triangle: hexakaidecagon (16-sided)
- ...
- 5×2n-sided
- 54°-36°-90° triangle: pentagon (5-sided)
- 72°-18°-90° triangle: decagon (10-sided)
- 81°-9°-90° triangle: icosagon (20-sided)
- 85.5°-4.5°-90° triangle: tetracontagon (40-sided)
- 87.75°-2.25°-90° triangle: octacontagon (80-sided)
- ...
- 15×2n-sided
- 78°-12°-90° triangle: pentakaidecagon (15-sided)
- 84°-6°-90° triangle: tricontagon (30-sided)
- 87°-3°-90° triangle: hexacontagon (60-sided)
- 88.5°-1.5°-90° triangle: hectoicosagon (120-sided)
- 89.25°-0.75°-90° triangle: dihectotetracontagon (240-sided)
- ... (Higher constructible regular polygons don't make whole degree angles: 17, 51, 85, 255, 257...)
- 3×2n-sided regular polygons, for n in 0, 1, 2, 3, ...
- Nonconstructible (with whole or half degree angles) – No finite radical expressions involving real numbers for these triangle edge ratios are possible, therefore its multiples of two are also not possible.
- 9×2n-sided
- 70°-20°-90° triangle: enneagon (9-sided)
- 80°-10°-90° triangle: octakaidecagon (18-sided)
- 85°-5°-90° triangle: triacontakaihexagon (36-sided)
- 87.5°-2.5°-90° triangle: heptacontakaidigon (72-sided)
- ...
- 45×2n-sided
- 86°-4°-90° triangle: tetracontakaipentagon (45-sided)
- 88°-2°-90° triangle: enneacontagon (90-sided)
- 89°-1°-90° triangle: hectaoctacontagon (180-sided)
- 89.5°-0.5°-90° triangle: trihectohexacontagon (360-sided)
- ...
- 9×2n-sided
Calculated trigonometric values for sine and cosine
The trivial ones
In degree format: 0, 30, 45, 60, and 90 can be calculated from their triangles, using the Pythagorean theorem.
n × π/(5 × 2m)
Geometrical method
Applying Ptolemy's theorem to the cyclic quadrilateral ABCD defined by four successive vertices of the pentagon, we can find that:
which is the reciprocal 1/φ of the golden ratio. Crd is the Chord function,
Thus
(Alternatively, without using Ptolemy's theorem, label as X the intersection of AC and BD, and note by considering angles that triangle AXB is isosceles, so AX = AB = a. Triangles AXD and CXB are similar, because AD is parallel to BC. So XC = a·(a/b). But AX + XC = AC, so a + a2/b = b. Solving this gives a/b = 1/φ, as above).
Similarly
so
Algebraic method
The multiple angle formulas for functions of 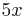 , where
, where 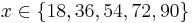 and
and 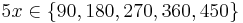 , can be solved for the functions of
, can be solved for the functions of  , since we know the function values of
, since we know the function values of 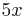 . The multiple angle formulas are:
. The multiple angle formulas are:
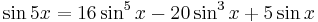 ,
,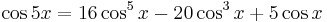 .
.
- When
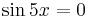 or
or 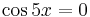 , we let
, we let 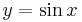 or
or 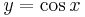 and solve for
and solve for 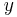 :
:
-
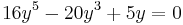 .
.
- One solution is zero, and the resulting 4th degree equation can be solved as a quadratic in
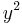 .
.
- When
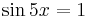 or
or 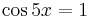 , we again let
, we again let 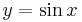 or
or 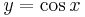 and solve for
and solve for 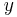 :
:
-
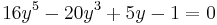 ,
,
- which factors into:
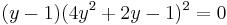 .
.
n × π/20
- 9° is 45-36, and 27° is 45−18; so we use the subtraction formulas for sine and cosine.
n × π/30
- 6° is 36-30, 12° is 30−18, 24° is 54−30, and 42° is 60−18; so we use the subtraction formulas for sine and cosine.
n × π/60
- 3° is 18−15, 21° is 36−15, 33° is 18+15, and 39° is 54−15, so we use the subtraction (or addition) formulas for sine and cosine.
Strategies for simplifying expressions
Rationalize the denominator
- If the denominator is a square root, multiply the numerator and denominator by that radical.
- If the denominator is the sum or difference of two terms, multiply the numerator and denominator by the conjugate of the denominator. The conjugate is the identical, except the sign between the terms is changed.
- Sometimes you need to rationalize the denominator more than once.
Split a fraction in two
- Sometimes it helps to split the fraction into the sum of two fractions and then simplify both separately.
Squaring and square rooting
- If there is a complicated term, with only one kind of radical in a term, this plan may help. Square the term, combine like terms, and take the square root. This may leave a big radical with a smaller radical inside, but it is often better than the original.
Simplification of nested radical expressions
In general nested radicals cannot be reduced.
But if for 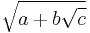 ,
,
is rational, and both
are rational, with the appropriate choice of the four ± signs, then
For example,
See also
- Trigonometric function
- Trigonometric identity
- Constructible polygon
- Trigonometric number
- 17-gonal construction
- Ptolemy's table of chords
- Niven's theorem
References
- Weisstein, Eric W., "Constructible polygon" from MathWorld.
- Weisstein, Eric W., "Trigonometry angles" from MathWorld.
- π/3 (60°) — π/6 (30°) — π/12 (15°) — π/24 (7.5°)
- π/4 (45°) — π/8 (22.5°) — π/16 (11.25°) — π/32 (5.625°)
- π/5 (36°) — π/10 (18°) — π/20 (9°)
- π/7 — π/14
- π/9 (20°) — π/18 (10°)
- π/11
- π/13
- π/15 (12°) — π/30 (6°)
- π/17
- π/19
- π/23
- Bracken, Paul; Cizek, Jiri (2002). "Evaluation of quantum mechanical perturbation sums in terms of quadratic surds and their use in approximation of zeta(3)/pi^3". Int. J. Quantum Chemistry 90 (1): 42–53. doi:10.1002/qua.1803.
- Conway, John H.; Radin, Charles; Radun, Lorenzo (1998). "On angles whose squared trigonometric functions are rational". arXiv:math-ph/9812019.
- Conway, John H.; Radin, Charles; Radun, Lorenzo (1999). "On angles whose squared trigonometric functions are rational". Disc. Comput. Geom. 22 (3): 321–332. doi:10.1007/PL00009463. MR1706614.
- Girstmair, Kurt (1997). "Some linear relations between values of trigonometric functions at k*pi/n". Acta Arithmetica 81: 387–398. MR1472818.
- Gurak, S. (2006). "On the minimal polynomial of gauss periods for prime powers". Mathematics of Computation 75 (256): 2021–2035. Bibcode 2006MaCom..75.2021G. doi:10.1090/S0025-5718-06-01885-0. MR2240647.
- Servi, L. D. (2003). "Nested square roots of 2". Am. Math. Monthly 110 (4): 326–330. doi:10.2307/3647881. JSTOR 3647881. MR1984573.
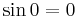
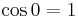
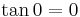
![\sin\frac{\pi}{60}=\sin 3^\circ=\tfrac{1}{16} \left[2(1-\sqrt3)\sqrt{5%2B\sqrt5}%2B\sqrt2(\sqrt5-1)(\sqrt3%2B1)\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/e05e0cfd3a6dc78847105d44fedd6d8b.png)
![\cos\frac{\pi}{60}=\cos 3^\circ=\tfrac{1}{16} \left[2(1%2B\sqrt3)\sqrt{5%2B\sqrt5}%2B\sqrt2(\sqrt5-1)(\sqrt3-1)\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/0a28eec32d1d9b3e4c9853d82f152789.png)
![\tan\frac{\pi}{60}=\tan 3^\circ=\tfrac{1}{4} \left[(2-\sqrt3)(3%2B\sqrt5)-2\right]\left[2-\sqrt{2(5-\sqrt5)}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/37d7ef279445c1b7a6b990d048be5a6d.png)
![\cot\frac{\pi}{60}=\cot 3^\circ=\tfrac{1}{4} \left[(2%2B\sqrt3)(3%2B\sqrt5)-2\right]\left[2%2B\sqrt{2(5-\sqrt5)}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/2f26fa8513f63069db0f7d38a51ef31c.png)
![\sin\frac{\pi}{30}=\sin 6^\circ=\tfrac{1}{8} \left[\sqrt{6(5-\sqrt5)}-\sqrt5-1\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/b2d584f2c42289e260b7766b81dc03b0.png)
![\cos\frac{\pi}{30}=\cos 6^\circ=\tfrac{1}{8} \left[\sqrt{2(5-\sqrt5)}%2B\sqrt3(\sqrt5%2B1)\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/1b9cab6a63b01679a9a301e553d901f9.png)
![\tan\frac{\pi}{30}=\tan 6^\circ=\tfrac{1}{2} \left[\sqrt{2(5-\sqrt5)}-\sqrt3(\sqrt5-1)\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/b22ef126e4939bd64f4faaa6e07b3467.png)
![\cot\frac{\pi}{30}=\cot 6^\circ=\tfrac{1}{2} \left[\sqrt3(3%2B\sqrt5)%2B\sqrt{2(25%2B11\sqrt5)}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/0cb52062f054bd52213a1ac1e9896b78.png)
![\sin\frac{\pi}{20}=\sin 9^\circ=\tfrac{1}{8} \left[\sqrt2(\sqrt5%2B1)-2\sqrt{5-\sqrt5}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/46032f976ea1ebba485c408606ba7518.png)
![\cos\frac{\pi}{20}=\cos 9^\circ=\tfrac{1}{8} \left[\sqrt2(\sqrt5%2B1)%2B2\sqrt{5-\sqrt5}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/4c22b68636a9bc251a413d40df6e7b71.png)
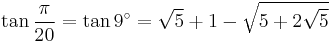
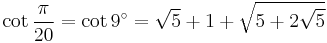
![\sin\frac{\pi}{15}=\sin 12^\circ=\tfrac{1}{8} \left[\sqrt{2(5%2B\sqrt5)}-\sqrt3(\sqrt5-1)\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/448dea307800fb78734a569455035e1f.png)
![\cos\frac{\pi}{15}=\cos 12^\circ=\tfrac{1}{8} \left[\sqrt{6(5%2B\sqrt5)}%2B\sqrt5-1\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/3cfa407103c20e018644c4e8580bea32.png)
![\tan\frac{\pi}{15}=\tan 12^\circ=\tfrac{1}{2} \left[\sqrt3(3-\sqrt5)-\sqrt{2(25-11\sqrt5)}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/f94b5f3281ee6be7bc380123cd66651a.png)
![\cot\frac{\pi}{15}=\cot 12^\circ=\tfrac{1}{2} \left[\sqrt3(\sqrt5%2B1)%2B\sqrt{2(5%2B\sqrt5)}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/aa8db3e5e51891aeba8de617c433352f.png)
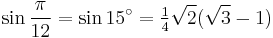
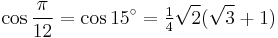
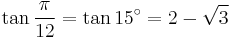
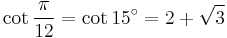
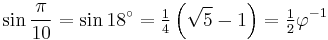
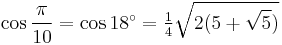
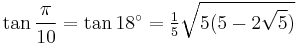
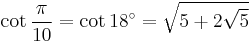
![\sin\frac{7\pi}{60}=\sin 21^\circ=\tfrac{1}{16}\left[2(\sqrt3%2B1)\sqrt{5-\sqrt5}-\sqrt2(\sqrt3-1)(1%2B\sqrt5)\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/63bd44f1682a0053223f322af23682e2.png)
![\cos\frac{7\pi}{60}=\cos 21^\circ=\tfrac{1}{16}\left[2(\sqrt3-1)\sqrt{5-\sqrt5}%2B\sqrt2(\sqrt3%2B1)(1%2B\sqrt5)\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/6d117676bd510ecebe796a5373e8c528.png)
![\tan\frac{7\pi}{60}=\tan 21^\circ=\tfrac{1}{4}\left[2-(2%2B\sqrt3)(3-\sqrt5)\right]\left[2-\sqrt{2(5%2B\sqrt5)}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/48ae55321d5a8958a1ad618b8e37f2d5.png)
![\cot\frac{7\pi}{60}=\cot 21^\circ=\tfrac{1}{4}\left[2-(2-\sqrt3)(3-\sqrt5)\right]\left[2%2B\sqrt{2(5%2B\sqrt5)}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/4562417970b44ac74328f31b334e3d31.png)
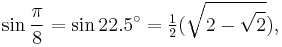
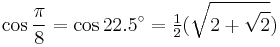
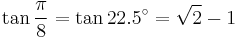
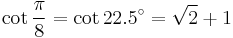
![\sin\frac{2\pi}{15}=\sin 24^\circ=\tfrac{1}{8}\left[\sqrt3(\sqrt5%2B1)-\sqrt2\sqrt{5-\sqrt5}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/88210bcd2c17bbe953ba486385da8bd5.png)
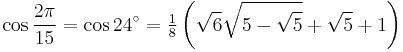
![\tan\frac{2\pi}{15}=\tan 24^\circ=\tfrac{1}{2}\left[\sqrt{2(25%2B11\sqrt5)}-\sqrt3(3%2B\sqrt5)\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/b87f950c9817114f8dd0f4972facbd84.png)
![\cot\frac{2\pi}{15}=\cot 24^\circ=\tfrac{1}{2}\left[\sqrt2\sqrt{5-\sqrt5}%2B\sqrt3(\sqrt5-1)\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/75e55ee371a92eed6e879900f54413b4.png)
![\sin\frac{3\pi}{20}=\sin 27^\circ=\tfrac{1}{8}\left[2\sqrt{5%2B\sqrt5}-\sqrt2\;(\sqrt5-1)\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/9116fcecd06bd4ca5b15b0b8206025ea.png)
![\cos\frac{3\pi}{20}=\cos 27^\circ=\tfrac{1}{8}\left[2\sqrt{5%2B\sqrt5}%2B\sqrt2\;(\sqrt5-1)\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/5aeab34c445536526a3ed815f9cb41a7.png)
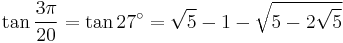
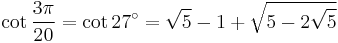
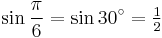
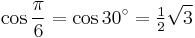
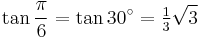
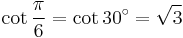
![\sin\frac{11\pi}{60}=\sin 33^\circ=\tfrac{1}{16}\left[2(\sqrt3-1)\sqrt{5%2B\sqrt5}%2B\sqrt2(1%2B\sqrt3)(\sqrt5-1)\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/287e90a61a40e1b2c8ca56fbf4a6a0a7.png)
![\cos\frac{11\pi}{60}=\cos 33^\circ=\tfrac{1}{16}\left[2(\sqrt3%2B1)\sqrt{5%2B\sqrt5}%2B\sqrt2(1-\sqrt3)(\sqrt5-1)\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/29f5add60c1c0a309a86a94037579f80.png)
![\tan\frac{11\pi}{60}=\tan 33^\circ=\tfrac{1}{4}\left[2-(2-\sqrt3)(3%2B\sqrt5)\right]\left[2%2B\sqrt{2(5-\sqrt5)}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/5eb24f58f05feabf3c96654d19aae65a.png)
![\cot\frac{11\pi}{60}=\cot 33^\circ=\tfrac{1}{4}\left[2-(2%2B\sqrt3)(3%2B\sqrt5)\right]\left[2-\sqrt{2(5-\sqrt5)}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/98335ba134c36c24f841fb41a21aa271.png)
![\sin\frac{\pi}{5}=\sin 36^\circ=\tfrac14[\sqrt{2(5-\sqrt5)}]\,](/2012-wikipedia_en_all_nopic_01_2012/I/92afb90a4135a46f97e2b114fd4ef2e6.png)
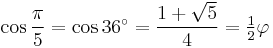
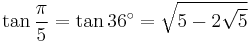
![\cot\frac{\pi}{5}=\cot 36^\circ=\tfrac15[\sqrt{5(5%2B2\sqrt5)}]\,](/2012-wikipedia_en_all_nopic_01_2012/I/8bd229892cba2f6317d0c642cfaea54d.png)
![\sin\frac{13\pi}{60}=\sin 39^\circ=\tfrac1{16}[2(1-\sqrt3)\sqrt{5-\sqrt5}%2B\sqrt2(\sqrt3%2B1)(\sqrt5%2B1)]\,](/2012-wikipedia_en_all_nopic_01_2012/I/23259ab19fa1e6e9618a1e77a9572fd0.png)
![\cos\frac{13\pi}{60}=\cos 39^\circ=\tfrac1{16}[2(1%2B\sqrt3)\sqrt{5-\sqrt5}%2B\sqrt2(\sqrt3-1)(\sqrt5%2B1)]\,](/2012-wikipedia_en_all_nopic_01_2012/I/7598fe0ef9f1dd60954e715fc323ef10.png)
![\tan\frac{13\pi}{60}=\tan 39^\circ=\tfrac14\left[(2-\sqrt3)(3-\sqrt5)-2\right]\left[2-\sqrt{2(5%2B\sqrt5)}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/5324d18bf95a4a0e647ef4faad869827.png)
![\cot\frac{13\pi}{60}=\cot 39^\circ=\tfrac14\left[(2%2B\sqrt3)(3-\sqrt5)-2\right]\left[2%2B\sqrt{2(5%2B\sqrt5)}\right]\,](/2012-wikipedia_en_all_nopic_01_2012/I/206a9f1259882d1858d9ece9dcf0e71d.png)